Крушение Римской империи заморозило прогресс криптографии. Шифры раннего средневековья так же примитивны, как и античные и легко взламываются любым любителем.
Ситуация меняется только в XV веке, начиная с работ Леона Баттисты Альберти и Иоганна Тритемия. Начинается использование шифров, позволяющих делать сложные замены серий букв на другие серии. При этом резко увеличивается количество возможных комбинаций, а значит, и сложность шифра. К сожалению, все шифры, разработанные до 1929 года неустойчивы к взлому частотным анализом. В этом году классическая работа Лестера Хилла позволила создать первый устойчивый шифр. Однако устойчивые алгоритмы слишком сложны для ручного шифрования, и с тех пор по сей день шифрование и дешифрование делаются машинным способом. Устройство шифровальных машинок и алгоритмы компьютерного шифрования мы рассматривать не будем по причине их невоспроизводимости примитивными технологиями попаданца.
Частотному анализу удавалось препятствовать при помощи омофонических кодовых таблиц. Буквы заменялись на одну из нескольких кодовых цифр. Часто используемым буквам соответствовало большее количество комбинаций. Это позволяет «размазать» частоту и затруднить взлом. К сожалению, такой метод не дает гарантированного результата. Даже увеличение таблиц до 50 тысяч строк не позволяло гарантировать устойчивость. Учитывая, что при этом необходима физическая защита таблицы замен, проще и надежнее использовать обычную кодовую книгу.
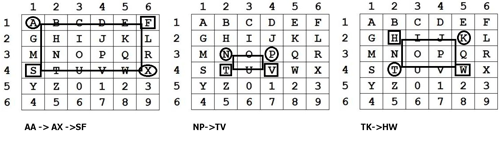Примером простого и устойчивого по меркам античности шифра будет шифр Плейфера, биграммный шифр замены. Берем квадрат Полибия, составленный с помощью кодового слова, берем буквы попарно. Если обе буквы одинаковы, заменяем вторую на условленную (например, Х, если обе Х — Я). Строим прямоугольник, симметричный относительно центра квадрата Полибия, углами которого будут наши буквы. Две буквы, расположенные в других углах, записываем в шифровку. Благодаря тому, что буквы заменяются попарно, количество возможных комбинаций составляет 600—900 вариантов. Слишком много для блестящих умов античности.
В позднем средневековье лучше использовать шифр Виженера. Посмотрим на описание шифра из Википедии.
В шифре Цезаря каждая буква алфавита сдвигается на несколько строк; например, в шифре Цезаря при сдвиге +3, A стало бы D, B стало бы E и так далее. Шифр Виженера состоит из последовательности нескольких шифров Цезаря с различными значениями сдвига. Для зашифровывания может использоваться таблица алфавитов, называемая «tabula recta» или «квадрат/таблица Виженера». Применительно к латинскому алфавиту таблица Виженера составляется из строк по 26 символов, причём каждая следующая строка сдвигается на несколько позиций. Таким образом, в таблице получается 26 различных шифров Цезаря. На разных этапах кодировки шифр Виженера использует различные алфавиты из этой таблицы. На каждом этапе шифрования используются различные алфавиты, выбираемые в зависимости от символа ключевого слова. Например, предположим, что исходный текст имеет вид:
ATTACKATDAWN
Человек, посылающий сообщение, записывает ключевое слово («LEMON») циклически до тех пор, пока его длина не будет соответствовать длине исходного текста:
LEMONLEMONLE
Первый символ исходного текста A зашифрован последовательностью L, которая является первым символом ключа. Первый символ L шифрованного текста находится на пересечении строки L и столбца A в таблице Виженера. Точно так же для второго символа исходного текста используется второй символ ключа; то есть второй символ шифрованного текста X получается на пересечении строки E и столбца T. Остальная часть исходного текста шифруется подобным способом.
Исходный текст:
ATTACKATDAWN
Ключ:
LEMONLEMONLE
Зашифрованный текст:
LXFOPVEFRNHR
Как взламывается такой шифр?
Шифр Виженера «размывает» характеристики частот появления символов в тексте, но некоторые особенности появления символов в тексте остаются. Главный недостаток шифра Виженера состоит в том, что его ключ повторяется. Поэтому простой криптоанализ шифра может быть построен в два этапа:
- поиск длины ключа;
- криптоанализ.
Одним из методов нахождения периода полиалфавитных шифров является метод, предложенный Фредериком Касиски в 1836 году. Он заключается в том, что в зашифрованном тексте находятся одинаковые сегменты длины не меньше, чем три буквы, затем вычисляются расстояния между первыми буквами соседних сегментов. Оказывается, предполагаемый период является кратным наибольшему общему делителю для этих расстояний.
Ключ:
ABCDAB CD ABCDA BCD ABCDABCDABCD
Исходный текст:
CRYPTO IS SHORT FOR CRYPTOGRAPHY
Шифрованный текст:
CSASTP KV SIQUT GQU CSASTPIUAQJB
Вы видите повторы последовательности CSASTP через 16 символов. Следовательно, длина ключа это делитель 16 — 2, 4, 16. Если найти еще несколько повторяющихся последовательностей, длина ключа будет известна. Можете попробовать самостоятельно определить длину ключа этой шифровки DYDUXRMHTVDVNQDQNWDYDUXRMHARTJGWNQD. Касиски полностью взломал шифр в XIX веке, хотя известны случаи взлома этого шифра некоторыми опытными криптоаналитиками ещё в XVI веке.
Опишем простой метод увеличить длину ключа. Берем кодовое слово и разбиваем его на отрезки, длиной в разные простые числа (3, 5, 7 и т. д.). Циклически записываем каждую последовательность и складываем строки.
Ключ: thatbigpassword
Разбиваем на 3, 5, 7 букв: tha tbigp assword
Записываем циклически:
thathathathathathathathathathathathathathathathathatha
tbigptbigptbigptbigptbigptbigptbigptbigptbigptbigptbig
asswordasswordasswordasswordasswordasswordasswordasswo
Складываем:
nbbwllxpycxptqpgbfoowuiygpsfnigfwrztnidxsecgikwzdwmnmu
Благодаря тому, что мы используем простые числа, ключ будет повторяться циклически с периодом, равным произведению чисел. Мы превратили 15-буквенный ключ в 3*5*7 = 105-буквенный, 26-буквенный в 1155-буквенный! Этот алгоритм достаточно устойчив к ручным методам взлома.
Пожалуй, совмещение этого метода и шифра Виженера будет наилучшим выбором для попаданца. Абсолютная устойчивость в средневековье при относительной простоте и малой длине ключа.
Если не требуется абсолютная секретность, то можно использовать примитивную шифровальную машинку. Берем 33 диска с алфавитом, написанным на краю диска в случайном порядке. Каждый диск обозначен своей буквой. Такое же оборудование должен иметь получатель. Надеваем на ось по порядку не меньше 10 дисков по буквам кодовой фразы. Поворачивая диски, составляем сообщение. Выбираем случайную горизонтальную строку и записываем ее в шифровку. При расшифровке исполнитель должен надеть диски по порядку, набрать шифрованную фразу и, поворачивая машинку, найти осмысленную последовательность. Такой метод шифрования имеет стойкость метода Виженера без алгоритма удлинения кодовой фразы, но намного проще в применении и обучении.
Если у вас имеется ноутбук и знания основ программирования, то успех гарантирован. Даже если на ноутбуке нет среды программирования, вы можете найти интерпретатор (в Windows это интерпретаторы Visual Basic’a и Java — WSCRIPT.EXE, CSCRIPT.EXE, в современных nix-овых системах практически всегда есть интерпретатор языка Питон), примеры скриптов (*.vbs, *.js в Windows). Вы сможете мгновенно делать частотный анализ текста и перебирать миллионы вариантов кода в секунду. При достаточной длине сообщения ни один практически применимый ручной метод шифрования не устоит перед компьютерной атакой.
Кто-то перечитался Нила Стефенсона 🙂
Гм. А как обеспечить зарядку ноутбука? Да и как объяснить шайтан-машину окружающим?
>> А как обеспечить зарядку ноутбука? Да и как объяснить шайтан-машину окружающим?
Мышки спросили у филина: «Как нам спастись от лисы?»
— Научитесь летать, как я.
— А как нам научиться летать?
— Стратегию я вам дал, а в тактике разбирайтесь сами.
На конце разьема питания в ноут идет 12 Вольт. Делаем Вольтов столб с пластинами пошире и постепенно наращиваем длину, повышая таким образом напряжение. Малое напряжение ноут не спалит, а как дойдем до 10-12 загорится лампочка зарядки.
А от окружающих ноут лучше прятать.
Про зарядку рассказано на примере мобилки
Только у ноута напряжение выше, и хорошо было бы знать какое именно надо — у того же эппла от модели к модели варьируется от 14 до 24 вольт, а вообще в большинстве случаев — 19 вольт.
Поэтому багдадских батарей для этого напряжения нужно много. На стандартные 19 вольт нужно 55 горшков.
Но тут проблема в том, что как правило нужно 5 ампер. Если тока не будет — ноут заряжаться не станет. Сколько раз нужно дублировать эти 55 горошков и подключать их блоками последовательно я не знаю. Скорее всего нужно сделать не меньше 150 горшков. Это дико дорого по тем временам, но ведь ноут же…
Напряжение указано на батарее. Для зарядки напряжение нужно несколько больше для корректной работы инвертера. К примеру, для стандартных 13,7-14,4 нужны как раз те самые 19 вольт.
Кроме того, зарядка будет идти при любом токе, вопрос лишь в ее скорости. Ну и 5 ампер это явный перебор — БП обычно имеют мощность в районе 60 Вт, это около 3А, причем это в режиме одновременной работы и зарядки
Напряжение проседает, да — но незначительно. Только если совсем плохой стабилизатор или с питалово пытаются взять больше тока, чем он может выдать, но тогда нормальный стабилизатор ограничивает вплоть до отключения.
А вот на счет «заряжается при любом токе» — это неверно в корне.
У вас, видимо, никогда не было планшета, который от того же USB с компьютера не заряжается, а только из розетки, потому что компьтер на USB не дает требуемого тока. И никогда не было ноута, который, будучи воткнут в автомобильный инвертор за четыре часа поездки ни на процент не зарядился (что самое интересное — инвертор работает и греется при этом).
Хотя, возможно, у вас ноут еще на сернисто-кадмиевых аккумах, ровесник нокии 5110, потому как все, что на ион-литии — больно умное и от слабого тока отказывается.
Мощности блоков питания зависят от диагонали экрана. На какой-нибудь ультрабук и 45 Вт может быть, а так все чаще до 90 Вт доходит. При этом на блоке питания того же макбук-про написано: 4.5 А.
Я как раз с такого планшета пишу. И зарядка при маленьком токе там отключается специально, так как 0.5 А для одновременной работы и зарядки не хватает и чтобы пользователь не питал лишних надежд. В нетбуках, заряжающиеся от собственного БП такой фичи нет.
90Вт БП в современных ноутах большая редкость.
На записке, зашифрованной шифром Виженера, построен сюжет «Жангады» Жюля Верна.
Только Жюль Верн его не ломал математически, а нашли кодовое слово (взяли последние несколько знаков, которые оказались именем-подписью).
Стоит отметить ещё один, довольно изящный на мой взгляд, метод шифрования текста — поворотную решетку http://cybern.ru/resheto-crypt.html Зашифрованный текст пишется в одну строку, для дополнительной стойкости в послание добавляются заранее оговоренное количество лишних случайных знаков. Если таблица размером, скажем, десять на десять, и послание написано в обратном порядке, то расколоть такой шифр — задача весьма непростая.
Да, метод простой и достаточной эффективный.
Но на мой взгляд для попаданца не очень применимый. Во-первых он требует либо хранения трафарета решетки(а с сейфами в средневековье напряженка), либо сложного алгоритма для генерации решетки по ключу(с исполнителями, способными его запомнить тоже напряжно).
Без добавления случайных знаков его стойкость явно ниже стойкости шифра Виженера(пример взлома http://hacktheplanet.ru/item/32), и польза от процедуры добавления случайных знаков может быть легко обнулена ленью или некомпетентностью исполнителя.
Я бы использовал его только для защиты быстро устаревающих(несколько часов — курьерская информация) военных секретов. Собственно, для этого он и использовался в последние пару столетий.
Надо спиратить простеюшую амерскую шифрмашинку на барабанчиках — компактна (карманного размера), надежна (нечего ломать), дает достаточно стойкий шифр для тактического использования — если гонца перехватят, то, к тому моменту, как шифровку дотащат до аналитика и он ее взломает, информация уже будет неактуальна. http://maritime.org/tech/csp488.htm
По сути эта машинка и реализует шифр с точки зрения взлома, схожий с шифром Виженера. Хотя случайный выбор строки добавляет стойкости(но и затрудняет расшифровку, тк надо увидеть осмысленную строку).
В принципе для нас — идеальный вариант.
>> шифровку дотащат до аналитика и он ее взломает, информация уже будет неактуальна
Ну, учитывая что мы говорим о периоде до 18 века, не факт что вообще взломают.
Вместо барабанчиков проще сделать плоский аналог — машину на полосках. В крайнем случае можно обойтись и без основания, а просто вырезать несколько полосок из дерева или картона, написать на них случайный набор букв и разложить рядом. Вместо прозрачных поперечных визиров, можно использовать картонки с прорезью, палочки или проволочки. Для уменьшения размеров можно писать алфавит на обеих сторонах полосок. Для удобства можно как-то скрепить полоски, лежащие в одном ряду (хотя бы проколоть дырочку и продеть проволочку).
Очень богатая тема. И для попаданца — излишне богатая. 🙂
Собссно, серьёзное шифрование/дешифрование просто не нужно.
Где-то до 19-го века шифрование и криптоаналитика была на уровне детского сада и «пляшущих человечков» Конан Дойля.
Применение даже простых высокоэнтропийных алгоритмов (типа банального дерева Хаффмана с заменяемыми таблицами) — вундерваффель вплоть до начала компутерной эры. RSA же — просто непобедим.
Более серьёзных шифров не нужно по одной простой причине: отсутсвия вычислительной техники и недостаточного населения Земли. 🙂
Развитый криптоанализ (когда атаке подвергаются более-менее вменяемые шифры) предполагает подавляющее, абсолютное превосходство атакующей стороне в вычислительной мощи. Не в интеллекте, а просто в вычислительной мощи. То есть, если для шифровки требуется абстрактный человеко-час, для взлома нужны миллиарды-триллионы-квинтиллионы человеко-часов.
И для любого вменяемого шифра (хоть DES из прошлого века) этот множитель настолько велик, что криптоанализ обречен.
Одного человека для шифровки найти можно. Триллион человек для взлома найти нельзя.
Если попаданец применяет матметоды и детерменисткий подход (когда алгоритм заведомо известен атакующему и криптостойкость определяется соотношением требуемой вычмощи защиты и нападения), защита будет выигрывать ВСЕГДА вплодь до появления мощных компов. И далее будет выигрывать в абсолютном большинстве случаев; как правило, взлом сейчас проводится только вне алгоритмов, каким-то другим методом. Скажем, ректотермальный криптоанализ — подходит.
И только в исключительном случае, когда сложность шифра ограничивается принудительно, а превосходство в вычмощи абсолютно, возможен брутфорс.
Не совсем понятна мысль.
>> Если попаданец применяет матметоды и детерменисткий подход (когда алгоритм заведомо известен атакующему и криптостойкость определяется соотношением требуемой вычмощи защиты и нападения), защита будет выигрывать ВСЕГДА вплодь до появления мощных компов.
Если нам нужен удобный шифр, то до развития техники хотя бы до уровня Энигмы, которая сделает шифрование простым делом, любой РАЗУМНО СЛОЖНЫЙ шифр ломается вручную.
Так-то факт того что кодовые книги при однократном применении дают не расшифроваемый результат понимали на интуитивном уровне и в средневековье. Но это такой гемморой составлять, рассылать и обеспечивать их безопсность…
Ничего подобного. Ещё раз: стойкие шифры основаны на бОльшей вычислительной сложности взлома по сравнению с шифровкой (скажем, основа RSA — то, что перемножить числа много проще, чем разложить число на простые множители).
Поэтому хороший алгоритм, который требует у агента на шифровку сообщения, скажем, час, подразумевает, что на взлом потребуется триллион человеко-часов. Что в докомпьютерном мире неприемлимо.
В мире с компами — варианты взлома шифра есть. Скажем, шифрует человек со скоростью 1 оп/с, а взламывает комп — с миллиардом оп/с. Или — шифрует процессор телефона с миллионом оп/с (причём, с запретом использовать ключ более 64 бит), а взламывает — суперкомп с криптомодулями на ASIC для этого алгоритма. Да, НЕКОТОРЫЕ возможности есть (и то, даже сейчас абсолютное большинство атак криптосистем обычно проходит на ином уровне — рвут там, где тонко, а не брутфорсят).
А в докомпьютерную эру если на взлом шифра по известному алгоритму уже чисто по математике требуется триллион человеко-часов (а на шифровку — 1 чел*час), то всё. Точка. Хана бобику, это сообщение зашифровать/расшифровать — ещё можно, а прочитать без ключа — никогда и никак. Людей не хватит.
RSA это прекрасно. А теперь представьте что на том конце дворник-таджик или офисный клерк и он вручную перемножает стозначные цифры. Как по вашему, он часто будет ошибаться и вас материть? На то что по вашему нужен час он потратит пару дней или отправит бесполезную мешанину.
Сделать деревянные диски для энигмы и водить палочкой туда сюда, отслеживая прохождение сигнала и вручную крутя диски несложно. Но на мой взгляд для практики попаданца это не подойдет.
RSA это к примеру. И на другом конце вовсе не обязательно (или даже обязательно не) дворник.
У людей не хватало знаний. С мозгом у них было всё в порядке. Но а, RSA в докомпьютерную эпоху неудобен. Но его непрошибаемость стОит иногда того.
>Сделать деревянные диски для энигмы и водить палочкой туда сюда,
>отслеживая прохождение сигнала и вручную крутя диски несложно.
Как можно реорганизовать диски Энигмы и алфавиты на них так, чтобы их записать в строки двумерного массива? Я никак не могу додуматься, как это сделать, чтобы не приходилось «водить палочкой туда сюда, отслеживая прохождение сигнала», а можно было по столбцу открытого текста спуститься вниз, отразиться и потом подняться вверх на зашифрованый символ. Я додумался только до того, что в строках алфавиты должны быть перемешаны, но что делать дальше никак не могу понять. Есть, правда, одна идея, но мне кажется, что она ошибочная: со строки «открытого» символа опускаемся на одну строчку вниз и в ячейке под ней видим символ. Определяем порядковый номер этого символа в алфавите и потом перепрыгиваем на столбик с этим номером, но уже на строку ниже. Поднимаемся так же образом. То есть, символ в ячейке я интерпретирую, как номер стоблика, на который нужно перейти в строку выше или ниже. Как Вы думаете?
> При достаточной длине сообщения, ни один практически применимый ручной метод шифрования не устоит перед компьютерной атакой.
В теории — да.
На практике для организации успешной компутерной атаки на _хороший_ шифр потребуется огромное количество «ручного» труда программиста-криптоаналитика (и «просто попаданца» будет недостаточно).
Что легко подтвердить прямым экспериментом: я делаю простую систему шифрации с парой бумажек (времязатраты — пару часов на создание шифра, десяток минут — на шифрацию достаточно длинного сообщения), Вы — пытаетесь взломать шифр. Я не буду ограничивать Вас ни в вычмоще, не во времени. Но Вы не сможете взломать совершенно любительский шифр за для Вас приемлимое время.
На практике сложную систему с десятками правил исполнители юзать не будут или будут регулярно ошибаться, а объемы текста которые надо шифровать это далеко не то что можно зашифровать за десяток минут.
>> При́нцип Керкго́ффса — правило разработки криптографических систем, согласно которому в засекреченном виде держится только определённый набор параметров алгоритма, называемый ключом, а сам алгоритм шифрования должен быть открытым. Другими словами, при оценке надёжности шифрования необходимо предполагать, что противник знает об используемой системе шифрования всё, кроме применяемых ключей.
Нет, правила могут быть просты (в смысле, трудоёмкость шифровки — малой), а алгоритм вполне криптостойким.
Пробуем? 🙂
Конечно, полностью опишу алгоритм, который буду пользовать.
Интересно.
Ключ, ессно, должен быть в 2-3 десятка символов, меньше десятка неинтересно — делаем скрипт и обычный перебор. Генератор песедослучайной последовательности на его основе? Достаточно простой, устойчивый к ошибкам исполнителя и анализу.
Может сразу алгоритм? Если надо я шифрующий скрипт напишу, можно сразу зашифровать какой-нибудь рассказик классиков.
Алгоритм:
1. Подготовительная фаза (если шпиён всё своё обязан нести в голове и только-только прибыл в резиденцию). Можно пропустить, если мы уже шифровали/дешифровали тут сообщение и продолжаем работу со следующим и/или шпиён гений/очень много тренировался. Это всего лишь вспомогательные таблицы.
Ключ представляет собой свёрнутое в строку дерево Шеннона (но, конечно, без требований Шеннона-Фано к построению дерева, мы же не сжимаем, а криптуем). Первым делом разворачиваем его в дерево. Поскольку многабуков, и для декриптовки сообщения конкретный способ хранения свёрнутого дерева в ключе не важен, я его опущу.
Получаем бинарное дерево, в котором вершинам соотвествуют буквы, цифры, знаки препинания, предлоги или целые слова (как построен ключ). Это пригодится при дешифровке. Если, допустим, дерево идёт слева направо, то единицы всегда соотвествуют ветке вверх, нули — ветке вниз. Это посзволяет при минимальной тренировке довольно быстро отслеживать путь к символам взглядом.
Из этого дерева выписываем буквы, символы и слова в порядке, который нам будет удобен при шифровке (к примеру: буквы по алфавиту, цифры по порядку, затем знаки препинания и слова; но необязательно так, вопрос лишь удобства и привычек конкретного человека).
Здесь рисовать псевдографикой дерево я не буду, но таблица будет выглядеть как-то так:
а — 0010
б — 00010101
в — 01000101
г — 1001001111
д — 011011
е — 0111
…
пробел — 010
пробел — 10111010111001001011
вражеский термоядерный реактор — 1011101011100101
Особо обращаю внимание, что и в дереве, и в сообщении возможна (но не необходима) избыточность. Например, в принципе, ничто не мешает записывать пробел двумя разными способами, равно как и ставить два пробела между словами в сообщении. Алгоритм это не оговаривает никак, это в воле составителя ключа или сообщения соотвественно.
Подготовка сделана.
2.
Для криптовки сообщения записываем подряд числа, соотвествующие соотвествующим буквам. Например, для кодирования «а вражеский термоядерный реактор не будет нам мешать» будет выписано последовательно
0010 010 1011101011100101 010 00010101… (и так далее)
Получим
0010010101110101110010101000010101… (и так далее)
В конце сообщения дописываем произвольное количество произвольно взятых нулей и единиц.
Получив такую шифровку, мы начинаем водить одним пальчиком/карандашиком/меткой по строке, другим (или взглядом) — по вершинам нашего дерева. Если дерево хорошо нарисовано, без особой экономии площади, то путь по дереву отслеживается взглядом, и на букву уходит пара секунд даже у нетренированного человека (то бишь, меня). Хвостовые символы, которые при расшифровке не дают однозначного символа или дают бессмыслицу просто игнорируем.
Ещё добавлю несколько не относящихся собссно к шифрованию вещей…
На практике можно сжать требуемое для записи шифровки место и записать её буквами/символами мместного алфавита и цифрами (применяя просто разбивку двоичных символов по 4-5 и запись буквами). Но зато при сохранении двоичной записи мы (если мы имеем достаточно развитую машинерию) мы можем автоматизировать как шифровку, так и расшифровку сообщения. Бинарный код по своей природе хорошо совместим с примитивными системами передачи информации и прекрасно совместим со стеганографией (мы можем скрыть сам факт общения, что немаловажно).
Кроме того, такой алгоритм даёт возможность шпиёну широко использовать ситуативно-зависимые ключи и реально сокращать объём сообщения.
Как-то так.
Упс, допустил ошибку в примере, когда дописал ещё один пробел: конечно, честное дерево так выглядеть не будет.
Если туда влез даже реактор то это как минимум маленькая брошюра.
Это не шифр. Это извращенная кодовая книга, которая потенциально немного уменьшает размер сообщения за счет усложнения процесса кодирования(листать страницы будет то еще удовольствие) и составления самой книги. Ах да, при единственной ошибке в записи, все последующее сообщение можно выкидывать. Не гемморойтесь и просто шифруйте книгой.
Шифром это было бы если бы был алгоритм получения дерева по ключу. А так — любой человек с брошюркой читает все сообщения в сети. А ленивые исполнители вскоре приловчатся писать сообщение ближайшими узлами дерева. Чем это грозит объяснять надо?
Реактор ради стёба. Нет, нет никакой кодовой книги. Алгоритм получения дерева из ключа могу изложить. Ключ, как и договаривались — 20-30 символов (Вы предложили, не так ли?). Никакой книги.
Да, конечно, при единственной ошибке запись можно выкидывать. Собссно, _любое_ высокоэнтропийное преобразование этим отличается. Хаос же.
Алгоритм шифрации у Вас есть (для взлома у Вас вся инфа).
Шифрую что-нить знаков так на пару тысяч и поехали? Ключ — 30 символов. Язык сообщения — русский.
И да,
http://popadancev.net.s3-website-us-east-1.amazonaws.com/shifr-dlya-popadanca/#comment-17296
Так давайте алгоритм, а то все толчем воду.
И еще и сложение 🙂 Заставить бы вас зашифровать/расшифровать пару десятков сообщений со штрафами за ошибки, быстро бы пришли в чувство. На практики такая вещь без мер для контроля ошибок малополезна.
Я вчера уж написал, сервер сглючил.
Идея такая: из ключа в столбец выписываются все буквы и символы (уникальные, в порядке включения). К ним дописываются оставшиеся (не входившие в ключ) цифры, оставшиеся (не входившие в ключ) буквы алфафита (в алфавитном же порядке), пробел, затем — все сочетания «согласная-гласная» из ключа (в порядке вхождения в ключевую фразу), затем — все слова из ключа. Начиная снизу им в качестве веса присваивается порядковый номер. Плюс, к весу прибавляется 10 на каждое вхождение буквы/символа в ключ.
По этому раскладу строится классическое дерево Хаффмана. Замечу, что там всего несколько десятков узлов, ни о какой «брошюре» и речи не идёт.
Если шпиён тупой, вносим жёсткое правило — сначала использовать по возможности целое слово, при неудаче — целый слог, при неудаче — буквы.
Умному шпиёну оставляем свободу действий (с учётом этой рекомендации).
Да, если нужно ради 10 символов проделать такую работу, это кажется время- и трудоёмким. У меня ушло больше получаса на подготовку дерева. Но во-первых, дерево в конкретном безопасном окружении готовится лишь однажды, во-вторых, значительно упрощается дальнейшая работа по шифрованию. То есть, именно длинные сообщения шифруются/дешифруются относительно быстро (минимум операций на символ: нашел — поставил).
Даже сложение — не беда, потому что если конечный итог пишется\делается ручками, то сознательному шпиёну всё равно нужно его переписывать (чтоб начало/конец токенов не выделялись из-за пауз в их написании).
Понятно. Те ключ 30 букв, дерево порядка 70 узлов — 33 буквы, 10 цифр, пробел-точка-запятая, узлов двадцать на сочетания «согласная-гласная» из ключа(почему просто не все двубуквенные), узлов 5 на слова. Тогда действительно уместится на листок. Чтож вы на брошюру обижаетесь после разговоров о реакторах 🙂
>> То есть, именно длинные сообщения шифруются/дешифруются относительно быстро (минимум операций на символ: нашел — поставил).
Символ найти легко, а двадцать-тридцать двубуквенных искать в дереве тот еще гемморой, нет?
Такое кодирование не обнуляет избыточность. Одно слово будет всегда превращаться в одну последовательность(ну с умным шпиеном в несколько, и то не все слова, размер текста для статистики увеличится в несколько раз). По нескольким десяткам самых популярных слов дерево вполне восстанавливается. Дополнительные 25-35 вершин на биграммы и слова чуть усложняют дешифровку, но не на порядок.
Циклическое сложение поверх добавит геммороя(не только криптоаналитику 🙂 ). Но слова в одном месте цикла опять таки будут отображаться одинаково. Те объем текста необходимого для анализа увеличится на длину сообщения. Те порядка раз в 30. Если найти тонкие зависимости, можно уменьшить.
На практике изза постоянных ошибок пришлось бы добавить как минимум маркеры границ предложений и это резко упростило бы анализ.
Я бы оценил объем текста для взлома — без сложения несколько килобайт, со сложением 1-2 сотни килобайт. Если посол каждый день пишет шифрованные отчеты по триста букв это 1-2 года переписки.
Если иллюзии еще сохранились, пишите скрипт шифровки-расшифровки, шифруйте мегабайтную(если без сложения с ключом то можно и 20-30 кб) книгу и кидайте мне скрипт и шифровку, я вам ее взломаю 🙂
Так посол за год-два хотя б таки ключи менять будет, нет? 🙂 Если у него такая активная переписка, может, ему кючи хотя бы раз в неделю менять? Из соображений общечеловеческой чистоплотности? 🙂
Разумеется, в одну. Беда для Вас в том, что одну, но короткую. Допустим, 70 узлов, 7 бит максимальная последовательность и Вы её будете ловить на пересечении с ключом? 🙂 У Вас чистая (ну вот по случайности) поймать искомую последовательность (которая, ессно, ни разу не будет означать пересечения) — 1/128. То есть, в меговом файле — ну очень дохрена. 🙂 Разгребать такое утомитесь.
В чём и прикол с бинарным алфавитом: слишком мало инфы даёт совпадение одиночного символа.
Иллюзии не у меня. 🙂
Да, давайте, напишу.
>Символ найти легко, а двадцать-тридцать двубуквенных искать в дереве тот еще гемморой, нет?
Зачем в «дереве»? Дерево — это для быстрой расшифровки.
Для зашифровки — таблица. В которой слоги и слова тоже стоЯт по алфавиту, проблем их найти глазом не составляет. Не так уж их и много, в общем-то.
>> Так посол за год-два хотя б таки ключи менять будет, нет? 🙂 Если у него такая активная переписка, может, ему кючи хотя бы раз в неделю менять? Из соображений общечеловеческой чистоплотности? 🙂
Если у нас есть надежное место для хранения десятков ключей не лучше ли тупо хранить там кодовую книгу? Достаточно частой заменой ключа можно оправдать самый ненадежный шифр.
Посол не спец по шифрованию. Он хочет уделять этому как можно меньше сил и памяти. А тут вы со своим шифром, непереносящим ошибок.
>> Разумеется, в одну. Беда для Вас в том, что одну, но короткую. Допустим, 70 узлов, 7 бит максимальная последовательность и Вы её будете ловить на пересечении с ключом? 🙂 У Вас чистая (ну вот по случайности) поймать искомую последовательность (которая, ессно, ни разу не будет означать пересечения) — 1/128. То есть, в меговом файле — ну очень дохрена. 🙂 Разгребать такое утомитесь.
А посчитать? Слово «что» встречается 13400 раз на миллион. С последующим пробелом это 4 символа, по 6.25 бит — 25 бит. Вероятность случайной встречи такой 26 битной последовательности это 1/32 миллиона. В мегабитном тексте их будет пара тысяч.
>> Иллюзии не у меня. 🙂
>> Да, давайте, напишу.
Ок. Я вижу мы не спорим что добавочное циклическое сложение увеличивает исключительно механическую работу. Я и так гроблю которые выходные подряд на всякую фигню, так что начнем с варианта без суммации — на него я уверен придется потратить в сумме не больше человеко-дня. Объем текста можно соответственно уменьшить. No offence intended, уверен что функция шифровки и дешифровки будут отлажены и проверены.
Народ, а если тупо WinRAR’ом пожать, даже без шифрования, дешифровщики времен WW2 смогут это осилить без знания алгоритма?
Нет. Но это какой-то странный случай: декриптовка человеком того, что зашифровал комп. Ясен пень, что имея в миллиарды раз больше вычмощь, защищающаяся сторона абсолютно неуязвима. «Человек с компом против человека» в защите непобедим. Только в обратную сторону человек имеет шанс, и сейчас мы спорим, насколько тот велик.
Да, кстати, объясните, чем грозит «писать сообщение ближайшими узлами дерева»? А то вот я искренне не понимаю.
Если у вас три узла с пробелами и только один на первой странице брошюры то в основном его и будут юзать.
Нет никакой «брошюры».
Кроме того, это вовсе не является бедой, как Вы думаете. В данном случае способ энтопизации — сведение информационной избыточности к минимуму. То есть, часто юзаемый пробел будет малобитным, а значит, плохо вычисляемым бегущим коррелятором. То есть, интересы «ленивого шпиёна» полностью совпадают с задачами безопасности шифра — и там, и там требуется чтоб наиболее часто употребляемые символы были короче.
И сразу предупреждаю: если я буду шифровать, я, разумеется, сделаю работу взломщика неудобной. Не надо ожидать, что мои двоичные токены будут 100% соотвествовать символам (а не словам или слогам), что у меня не будет избыточности в кодировке или что я не буду использовать неразрушающую избыточность в сообщении (несколько пробелов подряд, да).
Для описанной битвы — нужны ДВА попаданца :).
Старые же шифры телефоном ломаются — до появления шифроблокнотов любые (книги не пойдут, ключ неслучаен). Ручками же попаданческими — как повезёт, тут без особых бонусов.
И напротив — попаданец во времена ранней вычислительной техники (до 50х включительно) — принесёт неломаемые шифры. Ну, если хоть минимально в теме.
Было сделано утверждение «При достаточной длине сообщения, ни один практически применимый ручной метод шифрования не устоит перед компьютерной атакой.»
Мне оно кажется сомнительным. 🙂
Вообще то доказано, что при достаточной длине сообщения ни один реализуемый на компьютере шифр не может быть абсолютно стойким при наличии у противника компьютера хотя бы того же поколения. Вопрос времени на взлом и количества противников.
И кстати, тут дело не вычмоще.
Тут дело в том, что для взлома даже примитивного алгоритма, даже при наличии компа, даже при компутерных/криптографических знаниях выше среднестатистических, на взлом шифра уйдет неприемлимо много усилий. Потому что фазу написания взламывающей проги нельзя игнорировать: она времяёмка, она трудоёмка и она же наукоёмка, наконец.
Это сложно, по-настоящему сложно, это требует знаний значительно выше среднего, даже если у тебя есть комп, а у шифрующих — компа нет.
И даже интернет под боком — не есть 100% спасение, потому что знания в Сети нужно найти, освоить и применить.
>что у меня не будет избыточности в кодировке
Избыточность как раз помогает. Поэтому перед сжатием любого файла его и сжимают.
То есть перед шифрованием.
Да, чтобы сделать задачу интереснее, ключ зашифруем этим же алгоритмом (ещё одна подготовительная таблица) и сложим побитово с сообщением (если сообщение длиннее, то классически — циклически).
Двоичное сложение при минимальной практике выполняется очень быстро.
Мои извинения. Я сильно переоценил устойчивость вашего шифра в предыдущих постах. Потратив несколько пятитиминуток в течении недели на размышления(в таких делах неделя пятиминуток лучше одного сплошного рабочего дня) я пришел к выводу что устойчивость сложной версии будет порядка нескольких килобайт текста. А объем необходимых вычислений это десятки-сотни миллионов двоичных операций. Т.е. можно обойтись и без компа — налаженный ручной выч контейнер по типу того что использовались в Манхэттановском проекте из полусотни человек справится с делом за месяц-другой.
Ничего страшного. 🙂
Я думаю, корректировки ещё будут. 🙂
Давайте вернемся к этому, когда я найду время написать скрипты (у меня сейчас лёгкий напряг с работой). Мне по-прежнему кажется, что Вы сильно недооцениваете трудоёмкость криптоанализа даже в таком тепличном случае (известен алгоритм + огромная статистика + компутер с гигаопсами под рукой).
ping
Да, в ближайшее время точно.
Я помню. Честно. 🙂
НГ выходные на носу. Что может быть лучше ломания шифров под елкой…
БЛИН!
Я забыл. Напрочь. :\ На 6(!) лет.
Но как только — так сделаю, я по-прежнему уверен, что непобедимая вещь.
>Давайте вернемся к этому, когда я найду время написать скрипты (у меня сейчас лёгкий напряг с работой). Мне по-прежнему кажется, что Вы сильно недооцениваете трудоёмкость криптоанализа даже в таком тепличном случае (известен алгоритм + огромная статистика + компутер с гигаопсами под рукой).
Вообще то он её дико переоценил. Причём, для случая, когда нет ни знаний алгоритма, ни статистики.
Была в девяностых мода шифровать исполняемый код для защиты его от копирования. Ни один из тех шифров не продержался часа.
Причём, не с гигафлопсами, а всего навсего на спектрумах.
Дополню ещё, что сообщение теоретически невозможно взломать при длине ключа равной длине сообщения.
Сразу после появления книгопечатания появился способ шифрования с помощью книги — практически неломаемый (бо длина той же библии превышает длину многолетней переписки сурового шпиёна).
>> Дополню ещё, что сообщение теоретически невозможно взломать при длине ключа равной длине сообщения.
Если быть точнее, случайного ключа. Хотя нас такая тонкость не особо не интересует. Книжный цифр хорош, но в иные времена книга это примерно подержанный автомобиль на наши деньги(плюс трудно гарантировать что две рукописные копии будут иметь идеально совпадающий текст). Ну и хранить ключ в открытом доступе всегда плохая идея
>> Шесть требований Керкгоффса
>> Хранение и передача ключа должны быть осуществимы без помощи бумажных записей
Я ж написал про _книгопечатание_ (что подразумевает как наличие идентичных копий, так и относительную дешевизну книг).
Дешевизну относительно чего?
«Сразу после появления книгопечатания…» — ключевое слово «сразу». Долгие десятилетия после изобретения книгопечатания и даже после изобретения типографского набора тиражи печатных книг не превышали нескольких сотен. Чаще всего тираж был всего несколько десятков. СРАЗУ после изобретения книгопечатания тиражи исчислялись единицами экземпляров. Это, конечно, несколько больше, чем единственный экземпляр рукописной книги, но СРАЗУ после изобретения книгопечатания книги не стали резко дешевле и резко распространёнными. На это десятки и даже, местами, сотни лет.
Дешевизну относительно копирования с помощью переписывания. Тираж в единицы-десятки-сотни означает, что экземпляр в единицы-десятки-сотни раз дешевле.
До тех пор, пока спрос на несколько порядков превышает предложение, увеличение предложения всего лишь на порядок-два на цене не отразится.
Это недолго. Потому что для расширения рынка нужно повышать грамотность, а для этого нужны книги. Поэтому после осознания идеи рынок был забит мгновенно по меркам тех времён, за десятки лет. Без работы книгопечатники не сидели, но и цены были уже далеки от цены рукописей.
>Если быть точнее, случайного ключа. Хотя нас такая тонкость не особо не интересует. Книжный цифр хорош, но в иные времена книга это примерно подержанный автомобиль на наши деньги(плюс трудно гарантировать что две рукописные копии будут иметь идеально совпадающий текст). Ну и хранить ключ в открытом доступе всегда плохая идея
Самая большая беда книжного шифра в том, что можно перебрать все книги, имеющиеся у отправителя. Достаточно разок навестить его домашнюю библиотеку и переписать корешки. А автомобиль себе спецслужба может позволить новый и не один. Правило: «ключ/пароль записанный подарен противнику» отменяется только тайной комнатой, куда исключён физический доступ посторонних.
Тут правильно намекнули на случайность ключа. Всего сто лет назад общее количество книг было такое, что с книжными шифрами той эпохи справится любой современный комп за несколько минут тупым брутфорсом
>Дополню ещё, что сообщение теоретически невозможно взломать при длине ключа равной длине сообщения.
Сразу после появления книгопечатания появился способ шифрования с помощью книги — практически неломаемый (бо длина той же библии превышает длину многолетней переписки сурового шпиёна).
Вот только реальная длина ключа книжного шифра равняется длине каталога книг, а вовсе не текста книги.
Что-то тут никто не вспомнил про шифр Паттерсона. А простейшая ведь штука — число в качестве ключа, никаких сложений по модулю, не требует таблиц, и вообще, зная ключ, сообщение можно просто читать с листа.
В простейшем случае мы записываем сообщение столбиками, дополняем последний столбик мусором, чтобы получился ровный прямоугольник символов, а затем к каждой строке получившегося текста применяем rot(K[i]) — смещение на i-ю цифру ключа.
Если хотим усложнить — можем перемешать строки по десяткам (и записываем порядок строк в первую половину ключа) или дописать в начало и конец строк K[i] и 10-K[i] случайных символов соответственно.
Про все шифры не упомнишь.
Почитал про шифр Паттерсона — о нем похоже и вспомнили только благодаря статье в American Scientist. Двести лет его никто, кроме создателя не применял, потом расшифровали небольшой текстик(те статистики было минимум), причем взломщик утверждает что его можно было взломать и вручную.
В общем ничего приковывающего внимание не наблюдается.
Один из самых простых шифров был выполнен в виде текста записанного на ленте намотанной вокруг палки строго определенного диаметра. Для его прочтения потребуется всего лишь точно такая же палка или столбик
Угу. И хроноаборигены сделали машину для дешифровки — конус. Наматываешь на него послание — смотришь где буквы складываются в слова и наматываешь на палку такой же толщины.
Если попаданец будет реализовывать шифры такой сложности и надежности, то я бы ему засунул эту палку в… в одно место в общем. 🙂
Тут нужно не палку засовывать, а «дешифратор». 😀
При вводе дешифратора на 5 см шифр раскололся. B)
Между прочим, очень много шифров было расколото таким методом… 😀
http://lurkmore.so/images/7/77/Book3jl0.jpg
>Между прочим, очень много шифров было расколото таким методом…
Даже таким методом невозможно «вскрыть» шифр, если каждое сообщение шифровалось отдельным случайно сгенерированным паролем. Максимум «криптоаналитику» расскажут весьма примерное содержание писем. Но нужно понимать, что возможности проверить корректность пересказа нет и не будет. Можно попытаться сыграть в Funkspiel («радиоигра»), если будут найдены оставшиеся пароли, но нужно понимать, что в неё же сыграет и другой игрок, если поймёт, что агент скомпрометирован. А это не так то сложно устроить, если, например, дознавателю сообщить ложную подпись или ложный код «работаю без принуждения». Шифрообмен с «центром» в таком случае всё равно должен продолжиться, чтобы агента за ненадобностью не ликвидировали физически, но разговоры пойдут исключительно только о птичках и погоде.
А что если применить схему, использованную янки в годы второй мировой войны — применить язык малочисленного племени типа новахо? В Российской империи можно взять тех же чукч или якутов и на основе их языка забацать шифр.
это хорошо для радиосвязи или телефона. большинство мелких народов письменности не имеет.
Кроме того, данный способ хорош именно для оперативного применения, письмо расшифруют на раз, уж пару профессоров — специалистов по языкам найти можно. Как и представителя народа который переведет текст. Может через неделю, может через месяц, но переведет.
>это хорошо для радиосвязи или телефона. большинство мелких народов письменности не имеет.
Международный фонетический Вам в помощь.
//Международный фонетический Вам в помощь.
На котором придется еще научить писать этого представителя малой народности.
Что опять таки не исключает моего основного возражения- это трюк для оперативной связи. Все что имеет ценность и через месяц после передачи таким образом передавать глупо.
Этот способ гарантирует устойчивость пока о нем не знает противник. Как только известно — небольшие проблемы ему он составит, но и у нас ведь будет много геммороя с переводом ‘эсминца’ в ‘большую железную рыбу’. В современной теории криптографии такие трюки, основанные исключительно на секретности, не одобряются, а эта теория основана на опыте.
> современных nix-овых системах практически всегда есть интерпретатор языка Питон),
Питона как раз в никсах очень часто нет. Более того, если он не ставился специально, то гарантированно отсутствует. А поставлен специально может быть ровно в двух случаях: или в составе среды разработки на питоне, или в составе приложения, интерфейс которого предусматривает исполнение скриптов на питоне. Зато в любой системе должен быть компилятор C, чтоб она могла называться NIX-системой. Причём, именно такой, что «скормить» ему исходник можно без среды прямо с командной строки. А интерпретатору? Интерпретатору как раз не всякому. Часто интерпретатор или получает исходники только из среды, или сшивается с исходником, или с байт-кодом в единый исполняемый файл.
>Вы сможете мгновенно делать частотный анализ текста и перебирать миллионы вариантов кода в секунду.
Вот только выбирать их них расшифровку придется вручную оценивая читабельность. Иначе попаданец — это сам Тьюринг. Ну или сразу большой коллектив как минимум мелкомягких.
именнодлинныесообщенияшифруютсядешифруютсяотносительнобыстро
——-
юбпывапвпвтьглелекафайфуайкуцеукеуокеауасмцееноелшншдншшдншдшд
——————-
1 буква — номер страницы
2 буква — строка книги, библии к примеру, или песенки весёлой.
Разделения слов буквами только там где смыслы теряются.
>Нет. Но это какой-то странный случай: декриптовка человеком того, что зашифровал комп. Ясен пень, что имея в миллиарды раз больше вычмощь, защищающаяся сторона абсолютно неуязвима. «Человек с компом против человека» в защите непобедим. Только в обратную сторону человек имеет шанс, и сейчас мы спорим, насколько тот велик.
Я и кодировал вручную то, что комп должен был раскодировать, и раскодировал то, что закодировал комп. Для программиста, или хорошего математика это забава. Вот если комп именно шифровал, тогда вручную вскрывать толку действительно мало. И то не всегда. Я раза три зашифровал изображения случайными ключами. И, представьте, себе, посмотрев на результат, увидел и ключи, и что именно было зашифровано. Но к кодам, для защиты не предназначенным, это не относится в принципе.
Вот криптомашина Лейбница.. Не требует электричества, а по удобству работы соответствует Энигме. Хотя, конечно же, значительно уступает Энигме по криптостойкости. Могла бы быть изобретена и раньше 17 века. В оригинале валик имеет 6 шифроалфавитов, что неудачно, лучше бы их было 7 (простое число дает более максимальный цикл для любого шага смены алфавита от 1 до 6). Криптостойкость можно увеличить, если клавиши не подписывать, а расположить их в один ряд, рядом с доп.прорезью. А за прорезью добавить аналогичный валик с буквами. Тогда шифроалфавит будет определяться сочетание шифроалфавитов на двух валиках, т.е. их будет больше. Например, на одном валике 7, на другом 5, тогда общее число шифроалфавитов равно 7*5=35, если еще и шаг поворота валиков удачно сделать.
В рамках идеи.
карманная шифровальная машинка
состоит из 5(6,7… Н) плоских дисков разбитых на сектора закрепленных на одной оси.
Два внутренних содержат алфавит.
диски номер 2,3 и до Н-1 имеют отметку на одном из секторов (можно усложнить шифр добавив, например на каждый диск отметки семи цветов).
внешние содержат как буквы так и «шифровальные команды» вида (Д3 +2) (Д2 -3) (Д4 А)и т.п.
Ход шифрования:
Диски устанавливаются в исходное положение заданное текущим шифром. Например АШКМБ означает что А сектор первого диска Ш сетор второго и т.ддолжны стоять в ону линию.
Далее, как обычно выбираем нужную намбукву на внутреннем диске, смотрим какая буква на втором, записываем. А вот дальше начинается перестановка. Смотрим какой сектор третьего диска стоит напротив отметки на втором и выполняем шифровальную команду с этого сектора (например Д2+3 означает что нужно провернуть второй диск на 3 сектора по часовой, а Д4А означает что нужно четвертый диск переставить сектором А на отметку диска 3). Далее смотрим на отметку на диске 3, и выполняем команду в секторе диска 4 и т.д. до последнего диска.
Т.е. после выполнение всех команд диски сместатся на псевдослчайные углы. Зашифровываем следующую букву…
При расшифровке аналогично, только буквы ищем на втором кольце, а результат смотрим на первом.
Достоинства:
простота изготовления. Хоть бумажные делай.
достаточно легко использовать.
число вариантов ключа составляем число букв в степени количества дисков. Даже 4 диска это уже МНОГО для ручного перебора.
можно по желанию усложнять, например добавив цветные отметки и, соответсвенно используя в текущей щифровке только отметки нужного цвета (указанного в шифре) или просто увеличив число дисков
Ручной шифр LC4 и его модификация LS47: https://habr.com/ru/post/352448/ . Сильно желательно ознакомиться с процессом шифрования в оригинальной статье автора шифра (https://eprint.iacr.org/2017/339.pdf), так как в переводе, который опубликован на Хабре, он описан не совсем однознакочно. В статье на Хабре ознакомьтесь с парольно-ключевым преобразованием — оно прикольное.
Дополнение: дисковая шифромашинка, которая изображена на третьей картинке в этой статье — это шифратор Томаса Джефферсона (третьего президента США) и его стойкость сильно выше, чем у шифра Вижинера: 26! * 36!, так как алфавиты несвязаны. Полосковый шифратор, ссылку на который давали в комментариях выше (https://www.cryptomuseum.com/crypto/lugagne/transpositeur/index.htm), — это шифратор полковника Паркера Хитта. Принцип шифрования не изменился, но изготовление шифратора стало намного проще и дешевле. В Википедии «полосковый шифратор» называется M-138-A, а шифратор Томаса Джефферсона — M-94.